基于js-算法入门

ljt 2023/12/24 算法

# 一、前沿

亮点：

1、思维导图

2、工具推荐

3、参考资料

# 一、思维导图

三个思维导图：前面两个是什么语言都是通用的，第三个是基于js的，可以结合前面两个和js语言特点来实现。

这三个思维导图还是挺有保存意义的

# 计算机数据结构思维导图

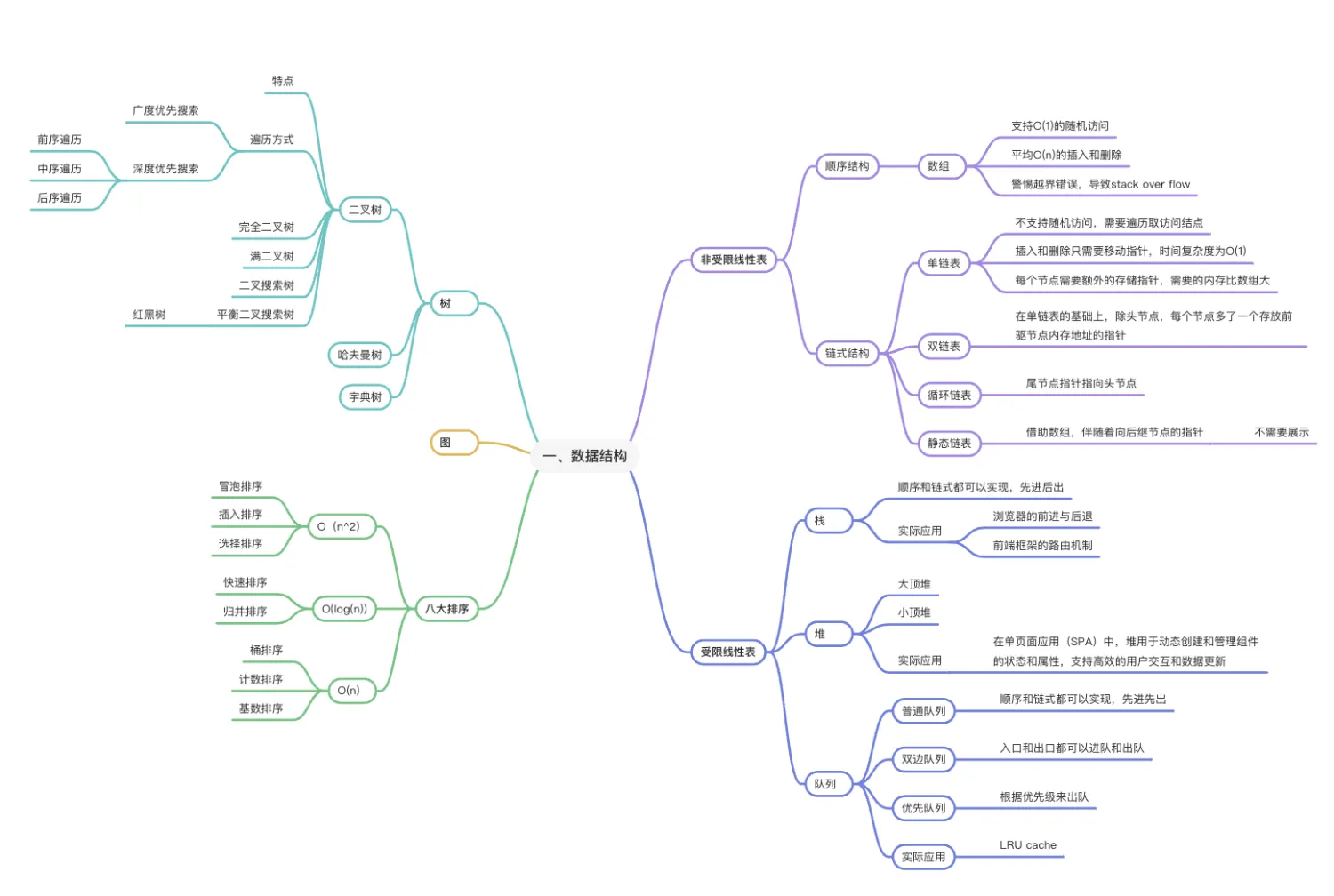
# 计算机算法思维导图

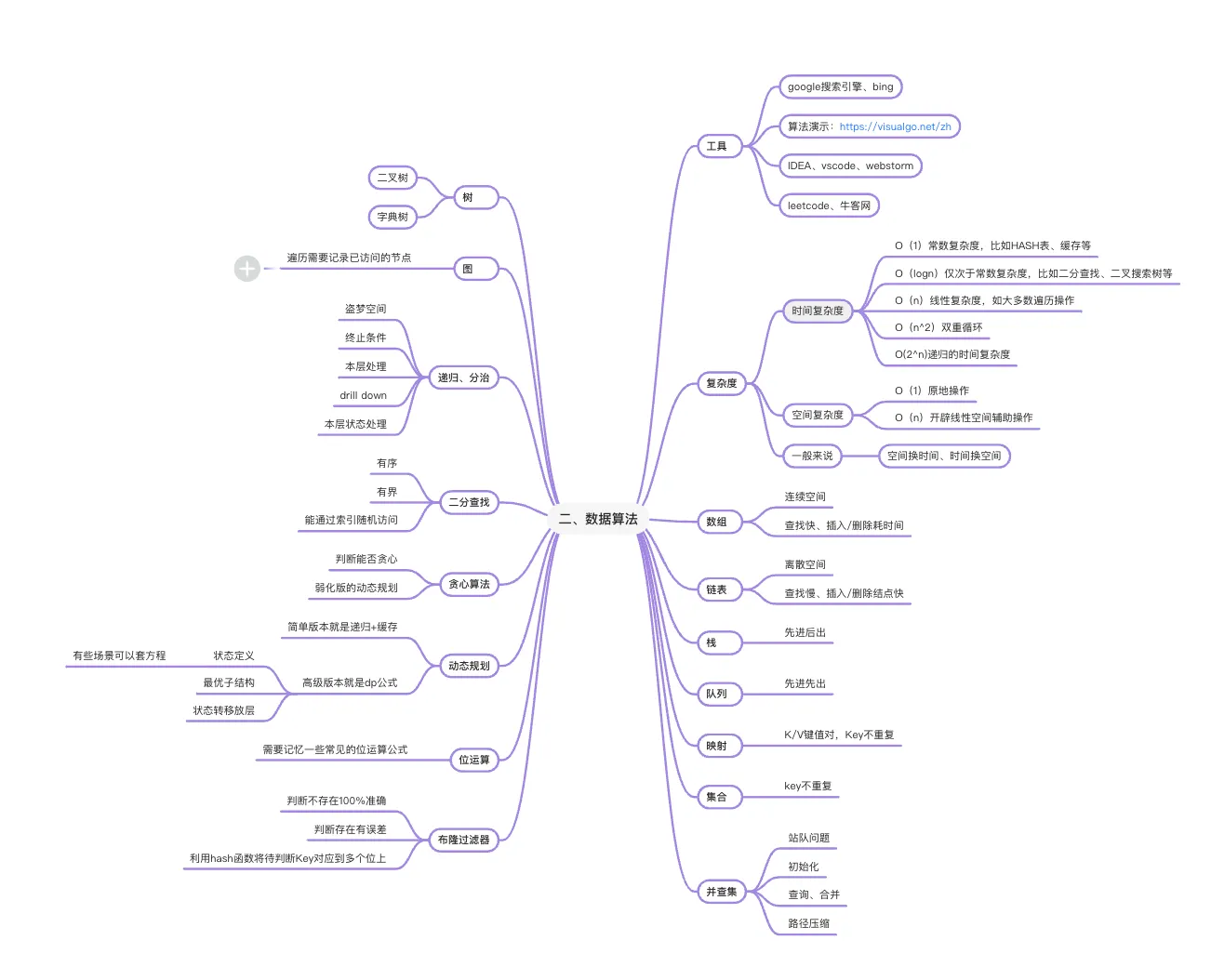
# JS数据结构

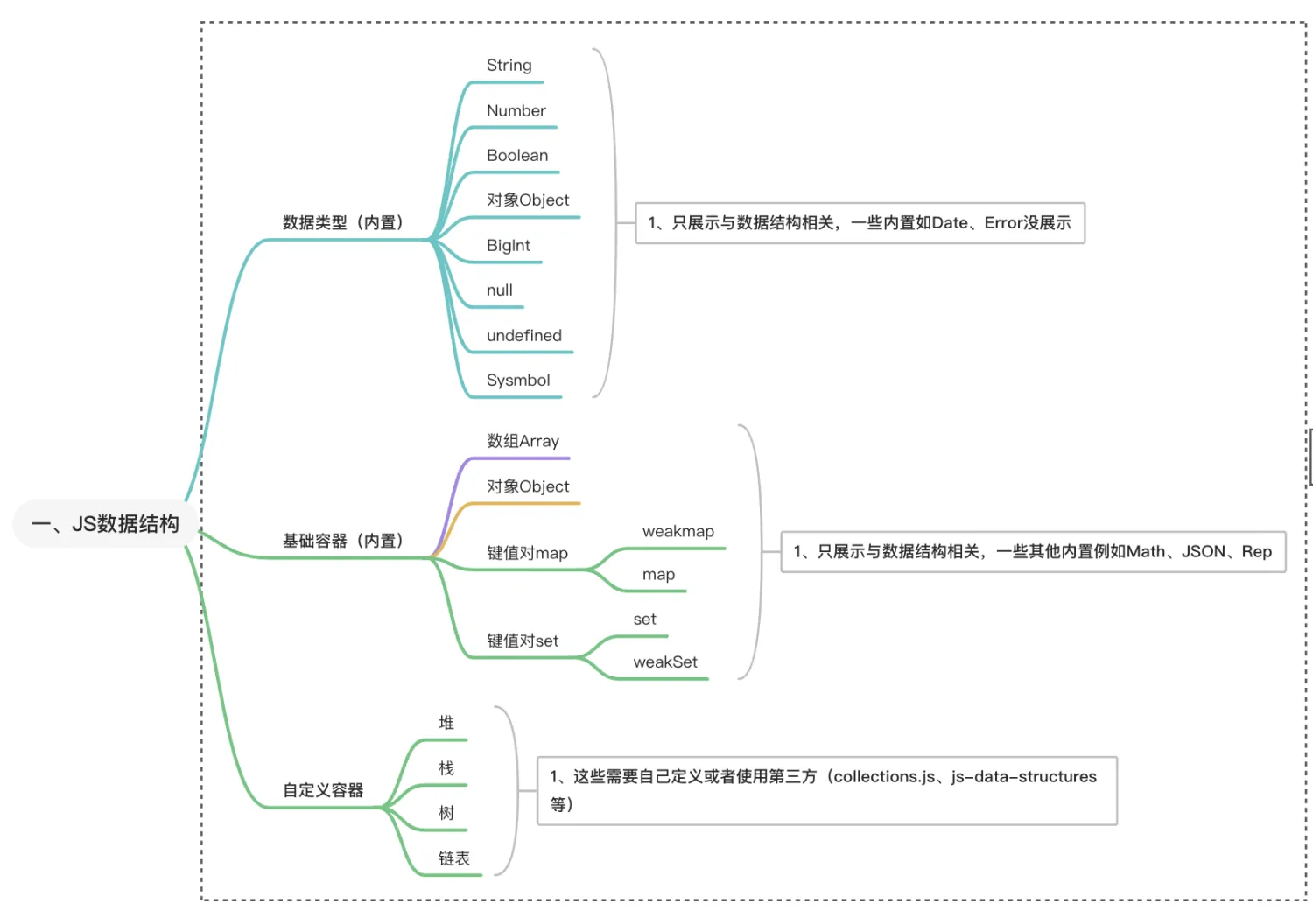
# 二、概要

了解数据结构后，了解算法，一般是一些常用的算法掌握了就差不多能应对大部分的。常见的就是排序算法、动态规划、贪心、窗口移动等等算法，围绕的主要是数组、链表，还有一些树的结构。

总结：

算法主要关注解决问题、时间复杂度、空间复杂度
算法通常来说都是时间换空间、空间换时间

# 三、工具

刷题工具：leetCode-cn、牛课网、leetCode

编译工具：vscode、webstorm、idea（非商用都免费）

算法可视化：https://visualgo.net/zh

# 四、递归/分治

# 分治

思路

归并排序的基本思路是：

将数组分成两半。
递归地对每一半进行排序。
将两个已排序的子数组合并成一个最终的排序数组。

基于js实现

function mergeSort(arr) {
    // 基本情况：如果数组长度小于等于1，返回该数组
    if (arr.length <= 1) {
        return arr;
    }

    // 分割数组
    const mid = Math.floor(arr.length / 2);
    const left = mergeSort(arr.slice(0, mid));  // 递归排序左半部分
    const right = mergeSort(arr.slice(mid));     // 递归排序右半部分

    // 合并已排序的子数组
    return merge(left, right);
}

function merge(left, right) {
    const result = [];
    let i = 0; // 左数组索引
    let j = 0; // 右数组索引

    // 合并两个已排序的数组
    while (i < left.length && j < right.length) {
        if (left[i] < right[j]) {
            result.push(left[i]);
            i++;
        } else {
            result.push(right[j]);
            j++;
        }
    }

    // 处理剩余的元素
    return result.concat(left.slice(i)).concat(right.slice(j));
}

// 使用示例
const array = [38, 27, 43, 3, 9, 82, 10];
const sortedArray = mergeSort(array);
console.log(sortedArray); // [3, 9, 10, 27, 38, 43, 82]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

操作

递归分割：mergeSort 函数首先检查数组的长度。如果长度小于等于 1，直接返回数组，因为它已经是排序好的。
合并步骤：merge 函数负责合并两个已排序的数组。通过两个指针分别遍历左边和右边的数组，将较小的元素放入结果数组中。
结果合并：最后，合并剩下的未处理元素。

总结

分治策略通过将复杂问题分解为简单子问题，从而利用递归简化解决过程。归并排序是分治算法的经典应用之一，适用于大规模数据的排序。

# 递归

概述：

递归是一种编程技巧，在函数内部调用自身以解决问题。使用递归的关键是确保每次调用都在向基例（终止条件）靠近，并能够有效地解决子问题。下面是一些经典的递归实现示例

例子：

function factorial(n) {
    // 基本情况：0! = 1
    if (n === 0) {
        return 1;
    }
    // 递归情况
    return n * factorial(n - 1);
}

// 使用示例
console.log(factorial(5)); // 120
function fibonacci(n) {
    // 基本情况
    if (n === 0) {
        return 0;
    }
    if (n === 1) {
        return 1;
    }
    // 递归情况
    return fibonacci(n - 1) + fibonacci(n - 2);
}

// 使用示例
console.log(fibonacci(6)); // 8

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# 五、贪心算法/动态规划

# 贪心算法

贪心是每次的最优解、动态是全局的最优解

概述：

贪心算法是一种通过局部最优选择来寻找全局最优解的方法。下面是一个简单的例子，使用贪心算法解决最少硬币问题。

function minCoins(coins, amount) {
    // 按照面额从大到小排序
    coins.sort((a, b) => b - a);
    
    let count = 0;
    
    for (let coin of coins) {
        while (amount >= coin) {
            amount -= coin;
            count++;
        }
    }
    
    // 如果amount为0，返回硬币数量，否则返回-1表示无法凑成
    return amount === 0 ? count : -1;
}

// 使用示例
const coins = [1, 5, 10, 25]; // 硬币面额
const amount = 63; // 目标金额
console.log(minCoins(coins, amount)); // 输出最少硬币数量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

总结：

在这个示例中，我们通过从大到小选择硬币，尽量用最少的硬币达到目标金额。这种方法在一些特定情况下是有效的，但并不适用于所有问题，因此在使用贪心算法时，需要确保其适用性。

# 动态递归

思路：

动态规划是一种解决问题的有效方法，特别适用于具有重叠子问题和最优子结构性质的问题。下面通过一个经典的例子——最长公共子序列 (LCS)，展示如何使用 JavaScript 实现动态规划。

function longestCommonSubsequence(str1, str2) {
    const m = str1.length;
    const n = str2.length;
    const dp = Array(m + 1).fill(null).map(() => Array(n + 1).fill(0));

    for (let i = 1; i <= m; i++) {
        for (let j = 1; j <= n; j++) {
            if (str1[i - 1] === str2[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }

    return dp[m][n];
}

// 使用示例
const str1 = "AGGTAB";
const str2 = "GXTXAYB";
console.log(longestCommonSubsequence(str1, str2)); // 输出 4

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

总结

动态规划通常用于解决优化问题，采用分阶段的策略，解决小问题并将其结果存储，以避免重复计算。通过自顶向下或自底向上的方式，我们可以高效地实现动态规划，显著提高性能。

# 六、排序算法

关于Array.sort

实际生产中，使用排序最多的是Array.sort()，

JavaScript 中的 Array.sort() 方法在不同的 JavaScript 引擎中使用不同的排序算法，但大多数现代浏览器（如 Chrome 和 Firefox）使用的是一种名为 Timsort 的算法。Timsort 是基于归并排序和插入排序的混合算法，旨在处理现实世界中的数据并优化排序性能。

# 时间复杂度

最坏情况：O(n log n)
平均情况：O(n log n)
最好情况：O(n)（当数组已经基本有序时）

Timsort 通过将数组分成小块（称为“run”），然后对这些小块进行排序，最后合并这些已排序的小块来达到高效排序的目的。因此，在处理部分有序的数据时，Timsort 的性能尤为出色。

值得注意的是，Array.sort() 方法的实现不一定是稳定的，这意味着相同元素的顺序可能在排序后发生变化。不同的引擎可能对此有不同的实现细节。

一般来说十大排序：

冒泡排序（Bubble Sort）

- 简单易懂，通过重复交换相邻的元素来排序。

选择排序（Selection Sort）

- 每次找到未排序部分的最小元素，放到已排序部分的末尾。

插入排序（Insertion Sort）

- 将元素逐一插入到已排序的部分，适合小规模数据。

归并排序（Merge Sort）

- 采用分治法，先分成小数组，再合并排序。

快速排序（Quick Sort）

- 选择一个“基准”元素，将数组分为两部分，递归排序。

堆排序（Heap Sort）

- 利用堆数据结构进行排序，时间复杂度较优。

计数排序（Counting Sort）

- 适用于范围较小的整数，通过计数实现排序。

基数排序（Radix Sort）

- 将数据按位数分组，逐位排序，适合大规模整数。

桶排序（Bucket Sort）

- 将数据分到多个桶中，再对每个桶内的数据排序。

希尔排序（Shell Sort）

- 通过间隔分组进行插入排序，逐步减少间隔。

# 参考资料

1、https://blog.csdn.net/weixin_46228563/article/details/138238235

2、https://visualgo.net/zh

忆梦世界

Choose mode